AI の需要予測を用いた在庫最適化

はじめに

DataRobot で小売・流通業のお客様を担当しているデータサイエンティストの新名庸生です。近年、AI を用いて需要予測に取り組まれるケースが様々な業界で増えてきています。需要予測に取り組むモチベーションは、経営計画やマーケティング計画への反映、物流センターでの人員の確保など複数ありますが、その中でも最も一般的な目的として在庫の最適化があります。ただ、需要予測ができたからといって在庫管理まで一足飛びにできるわけではありません。本稿ではまず需要予測と在庫の関係を考察し、続いて在庫最適化をスケールさせるために DataRobot でできることをご紹介します。

需要予測モデルと在庫

需要予測の精度と在庫の関係性

需要予測の精度を高めることによって、より在庫を最適化する事ができます。まずはこの点について仮想例を元に考察します。

あるレストランが翌日の来客数の予測を行っていたとします。このレストランでは1日前に翌日の来客数を予測し予測値に応じて食材を発注、翌日朝一で食材が届きます。また、当日使い切れず余った食材は破棄します。

このレストランのKPIは以下の2つであるとします。

1. 廃棄食材量：何人分の食材を廃棄するかで計算
2. サービス率：食材の欠品を出さずに利用者に食事を提供できる率（日単位で計算）

レストランでは、サービス率について目標値を定め、そのサービス率を達成するために生じる廃棄食材量を最小限に抑えたいと考えています。

毎日の来客数は1〜20人で、来客数が1人, 2人,…, 20人である確率はいずれも5%で同確率であることがわかっています。（図1）

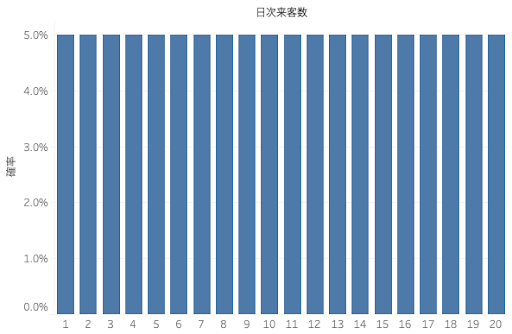
このレストランでは毎回翌日の来客数をこの分布の平均値である10.5人と予測していますが、サービス率90%（＝20日間のうち、食材に欠品を出さない日が18日あることに相当）を目指すために7.5人分を安全在庫として合わせて合計18人（=20人×90%）分の食材を発注しています。

レストランはある時、過去平均だけでなく天候という特徴量も考えながらより予測の精度を上げようと試みました。実はこのレストランの来客数は図2のように天候によってはっきり分かれており、雨の日は1人~10人が、晴れの日は11人~20人が同確率の10%で来客します。（簡単のため、天候は晴れか雨しかなく、晴れの日と雨の日は年間で同日数であるとします。また、天気予報は必ず当たるとします。）

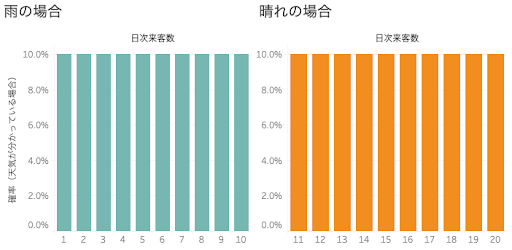
この時、翌日の天気を加味して精度を上げた需要予測はどれだけ廃棄食材量にインパクトをもたらすでしょうか。

まず、天気予報で翌日が晴れだと分かっている時、レストランは晴れの日の来客数分布の平均値の15.5人で来客数を予測します。サービス率は変わらず90%（10日間のうち、食材に欠品を出さない日が9日間あることに相当）を目指す場合、来客数が11人~19人のパターンをカバーする必要があるので、安全在庫の3.5人分を合わせて19人分の食材を発注します。翌日が雨だと分かった場合も同様に、レストランは雨の日の来客数分布の平均である5.5人と予測し、サービス率90%を達成するため、3.5人分の安全在庫を合わせて9人分を発注します。この時点で、サービス率を保ったまま安全在庫を7.5人分から3.5人分に圧縮できていることが分かります。

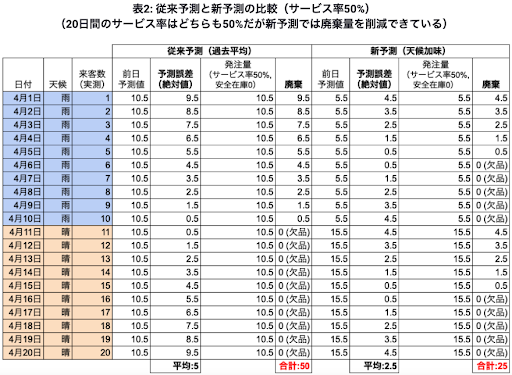
表1に4月1日から4月20日の20日間において前半10日が雨、後半10日が晴れで、来客数がそれぞれ1人, 2人, …, 20人だった場合のシミュレーションを掲載します。

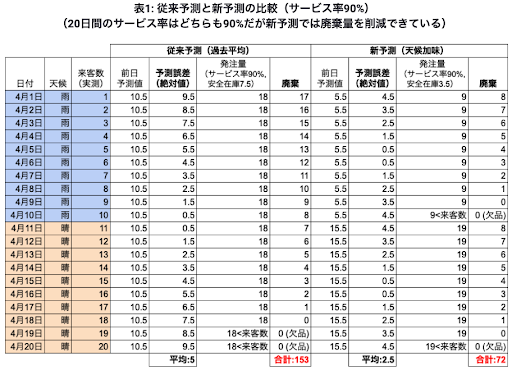
従来の予測（天候が加味されていない予測）だと20日間の予測精度が平均絶対誤差が5人で、153人分の廃棄が出ていたものが、天候情報を加味してより精度を上げた予測を行う事により平均絶対誤差が2.5人となりサービス率を変えずに72人分の廃棄に留めることができました。（晴れの日だけに着目すると廃棄量は増加していますが、同時にサービス率が80%から90%に改善されています。晴れの場合の予測精度が下がったわけではないため注意が必要です。）この表をわかりやすく可視化したものが図3になります。青色の三角形が従来の予測を行ったときの廃棄量、オレンジの2つの三角形が予測精度を上げた場合の廃棄量になります。

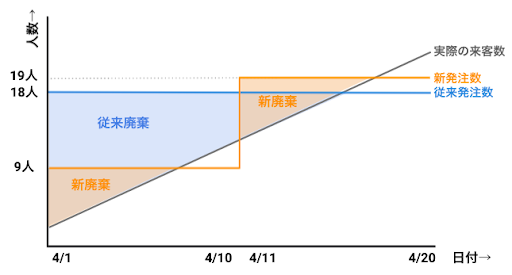
仮に安全在庫を持たなかった場合のシミュレーションも見てみましょう。この場合でも来客数が予測値以下の際に廃棄する食材の量を減らすことが出来ます。

こちらも晴れの日だけに注目すると新予測の方が廃棄が多く改善されていないように見えますが、そもそも従来の予測の場合は晴れの日のサービス率は0%でした。廃棄だけに着目してこれを最小にするには発注をゼロにすれば良いということになってしまいますので、廃棄量の少なさが直接予測精度を表すわけではない点に注意が必要です。実際、晴れの日だけに着目しても従来予測の場合、平均絶対誤差は5人、新予測の場合2.5人です。

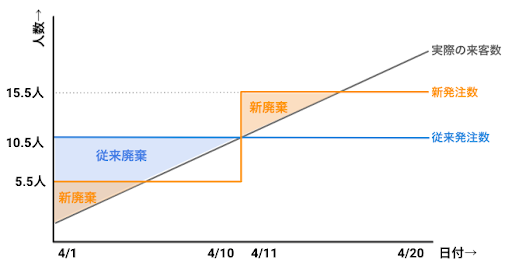
このように、よりきめ細かく予測して発注量をコントロールすることで、より少ない在庫で同じサービス率を維持できるようになります。

予測誤差分布を用いた安全在庫適正化

上記の天候を加味した予測では雨の日と晴れの日の需要分布が過去のデータから分かっていると仮定し、それを使ってサービス率90%を目指す場合はそれぞれ9人、19人と算出しましたが、実際は特徴量の値に応じた需要の分布が予め分かっているわけではありません。需要分布が未知の場合、予測誤差（ = 実測 – 予測 ）の分布からサービス率に応じた安全在庫と発注量を見積もることになります。例えば翌日が雨の日は4人、晴れの日は14人という予測を行っていた時、観測できる予測誤差は-3, -2, …, 5, 6で、予測誤差の分布は下図のようになるでしょう。

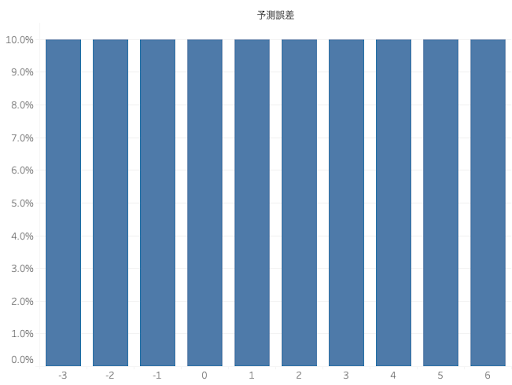
この予測誤差の分布の90%をカバーできるように安全在庫を持てばサービス率90%が実現できます。図から予測誤差は5まで見ておけば分布の90%はカバーできることが分かりますので、サービス率90%を達成するには安全在庫は5人分、発注量は予測値に安全在庫分を加えた値、すなわち雨の日は4+5=9人分、晴れの日は14+5=19人分と決定することができます。

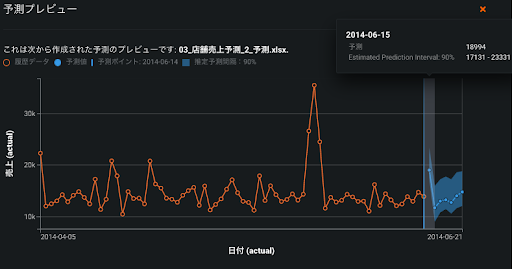
このようなニーズに合わせて DataRobot では予測を行う際に予測値だけでなく、モデルの構築過程で算出された予測誤差に基づいた予測区間を出力することができます（図6の青い範囲）。例えば予測区間を80%と指定すれば予測誤差分布の下位10%と上位10%（図5における-3と6）を除いた80%（-2~5）の誤差の可能性を考慮した範囲を算出します。雨の日は4人、晴れの日は14人という予測を行っていた場合、80%予測区間はそれぞれ[2(=4-2), 9(=4+5)]、[12(=14-2), 19(=14+5)]となります。サービス率とは違い予測区間はその名の通り区間であるため、下限も存在する点に注意が必要です。

最適なサービス率・発注量の推定

予測精度を上げられるとより少ない安全在庫で同じサービス率を維持できることは分かりましたが、維持すべき最適なサービス率、そして最適な発注量はどのように求められるでしょうか。この章ではまず前掲のレストランの例に当てはめることができる「新聞売り子モデル」を使った理論的アプローチを考察します。新聞売り子モデルでは損失を最小にするサービス率が公式として求められていますが、その式を用いるだけだと納得感に欠けるため、求めたサービス率に近いほど損失が小さくなることを可視化して確認します。しかし新聞売り子モデルはあくまでも数理的なモデルであり汎用性の観点では十分ではありません。そこで十分な量の実績データが利用可能な場合に実現可能な方法としてデータドリブンアプローチをご紹介します。こちらは最適なサービス率の導出を経ずに過去の発注量と損失のデータから直接最適な発注量の推定を行うアプローチです。ただ、データドリブンアプローチも必ずしも常に実現可能とは限りません。本章の最後ではデータドリブンアプローチの課題と実際のビジネスにおける最適な発注量へのアプローチの方向性について言及します。

理論的アプローチ

まず、理論的なアプローチについてご紹介します。前章までのレストランの例のようなケースは「新聞売り子モデル（Newsvendor model）」としてその解が数学的に求められています。具体的には、商品あたりの仕入コストを c 、販売額をpとしたとき、最適なサービス率は (p-c)/p であることが知られています。（新聞売り子モデルには廃棄コストも考慮した拡張もありますが今回は最もシンプルなケースで考えます。）証明は文献[3]などに譲り、ここでは極端な場合を考えてみます。もし仕入れコスト c が0の場合、最適なサービス率は100%であり、直感通り可能な限り入荷したほうが良いことになります。c=pの場合、売れたとしても利益が出ないため売れ残り損失を考えると最適なサービス率が0%であるのは納得がいきます。例えばレストランの例で1人前の食費の仕入れコストが3,100円、提供価格が10,000円だった場合、最適なサービス率は(10,000-3,100)/10,000=69%ということになります。その時の発注量は図1の需要分布より20×0.69=13.8人分となります。前述のように現実世界で需要分布が事前に分かっている場合は稀ですので、実際は予測誤差からサービス率69%に対応した発注量を見積もる必要があります。

公式に当てはめただけですとこれが最適であるという実感に乏しいため、シミュレーションでも確認しましょう。発注数が q 人分(1≦q≦20)で実際の需要がd 人(1≦d≦20)のとき、d≦q なら(q-d)*c の売れ残り損失が、q≦d の場合は(d-q)*(p-c)の品切れ損失が出ます。c=3,100、p=10,000として発注数 q を1≦q≦20の範囲の整数で動かしてみるとき、各 q で実際の需要 d が1~20の値を取る確率はそれぞれ5%であることを考慮して品切れ損失、売り切れ損失、その合計の損失の期待値をシミュレーションすると図7のようになります。

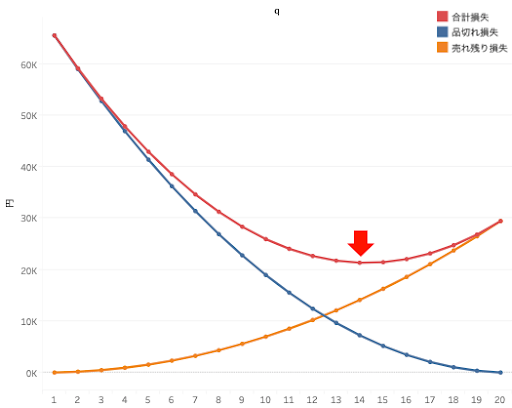
このシミュレーションでは q=14のときに合計損失が最小になっています。ここでは q を整数で動かしているためちょうど13.8ではありませんが、このシミュレーションからも先程の新聞売り子モデルによるアプローチの結果がもっともらしいことが分かります。

データドリブンアプローチ

新聞売り子モデルは実ビジネスで活用するには難しいポイントがいくつかあります。まず、需要分布が未知の場合、予測誤差分布から発注量を推定するという手間がかかります。また、例えば商品が売れ残りそうな場合は販売価格を徐々に下げていき売れ残りを減らそうとする施策はよく行われることですが、このように販売額 p が変化し、それに伴って変化する需要分布もあわせて考慮するのは困難です。こういった、理論だけでカバーするには複雑すぎる場面に適用可能な方法としてデータドリブンなアプローチを検討することができます。事象の裏にある理論を追究するのでなく、データとして現れている関係性を直接機械学習モデルに学習させるというアプローチです。例えば、データドリブンアプローチを取るには単純な例となりますが、先程理論的アプローチで導いた最適発注量 q をデータドリブンアプローチで求める場合は以下の手順となります。

1. 過去の実績データを用い、発注量（特徴量）から合計損失（ターゲット）を予測するモデルを作成
2. 作成したモデルを使って様々な特徴量の組み合わせを試し、合計損失を最小化する特徴量を推定

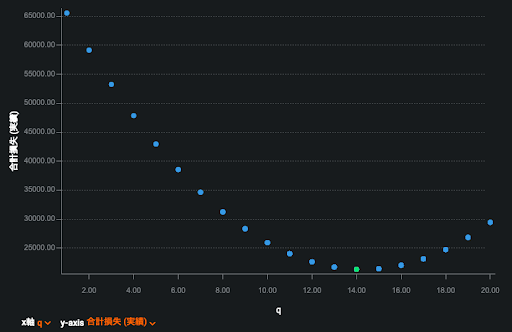
図8は以上の手順を DataRobot によるモデリングと最適化アプリケーションを用いて導出した結果です。こちらの手法では図1のような需要分布の情報は直接は使っていませんが理論的アプローチと同様に最適な発注量として14を発見することができています（q に整数という制限をかけて探索）。

現実的アプローチ

上記のデータドリブンアプローチもすべての場合に適用可能なわけではありません。例えば品切れしているかどうかに関わらず発注伝票が顧客から届く場合には品切れ損失は計算可能かも知れませんが、スーパーの棚に陳列されている食品などの場合は品切れ後にどれくらいの需要があったのか測定することは困難です。品切れが他の代替商品の購買につながる場合もあり、品切れをひとくくりに損失と捉えることができない場合もあります。このようにすべての場合に適用可能な最適発注量の導出方法はなく、実際のビジネスではシミュレーションや試行錯誤のなかでそれを推定していく必要があります。ただ、理論的アプローチやデータドリブンアプローチが全く活用できないわけではなく、何らかの仮定を設けてこれらのアプローチを応用しスタート地点とすることで、闇雲に行うよりも効率的な試行錯誤につなげることができます。

需要予測をスケールさせるための AI 活用（DataRobot を例に）

上記の最適化アプリケーションの例のように、AI は十分なデータが有ればそこから統計的な関係性を読み取った上で予測値や最適解を導出できるため非常に強力な味方となります。実際に DataRobot を用いて複雑な需要予測タスクを効率よくスケールさせられることを以下にご紹介します。

多商品に対する需要予測モデルの作成

レストランでの需要予測の例では天候という新しい特徴量を加えることで予測精度が上がりました。このように予測対象の過去の履歴だけではなく関連する他の特徴量も取り込むことで精度向上に繋げられるのが機械学習モデルの強みです。DataRobot では派生特徴量の生成という時系列特有の特徴量の前処理を自動で行った上で様々なアルゴリズムの機械学習モデルを作成できます。

また、異なる SKU であっても需要トレンドが同じである場合はまとめてモデリングを行った方が個々の SKU に対して別々のモデリングを行うより効率が良く、またデータ量としても増加するため精度向上につながる可能性があります。DataRobot では複数時系列モデリングにより最大100万系列を含む時系列データを一度に学習し、予測値を算出することができます。

精度のモニタリング

需要予測モデルは運用開始後、定期的に精度を確認しておく必要があります。刻一刻と変化し続ける環境下ではいつ需要トレンドに変化が起きるかわかりません。そのためには複数の実運用中のモデルの精度を横断的に監視し、かつ精度が悪化していれば原因の特定やモデルの作り直しなどを考える必要があります。DataRobot では実運用化されているモデルを一括して管理し、精度が悪化していればいち早く気付けるようにアラートのメールを設定しておくこともできます。

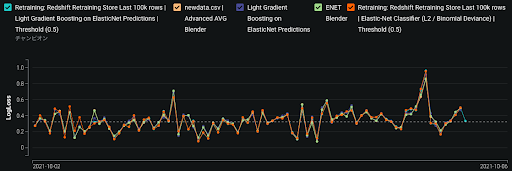
また、実運用モデルと並行して精度監視の対象とするチャレンジャーモデルを設定することができます。これはもし運用していればどれくらいの精度になっていたかをシミュレーションしたい際に設定できるもので、現行モデルとの比較を行うことができます。仮に現行モデルで大きな精度悪化が生じたとしてもチャレンジャーとして登録しているモデル（例えばロバスト性を重視して作成したアンサンブルモデル）でそれほど精度に変化がなかったものがあれば、取り急ぎそちらに運用を切り替える事ができます。

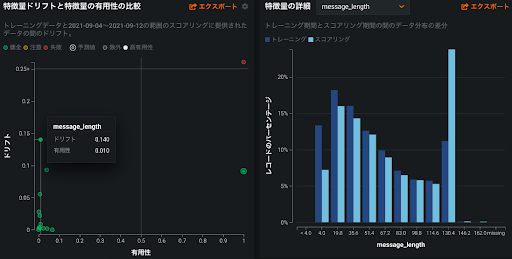
特徴量のドリフト（データドリフト）による原因調査

精度の悪化が起こった場合、学習で使ったデータと実運用で予測対象となったデータで大きく分布が異なっていることが一つの原因として考えられますが、具体的にどの特徴量の分布が異なっているのかを特定することは問題の理解や現場への説明に役立ちます。DataRobot では特徴量ごとにデータドリフトの度合いを視覚化できるので、学習データの分布と予測データの分布の乖離を確認することができます。

モデルの自動生成と置換

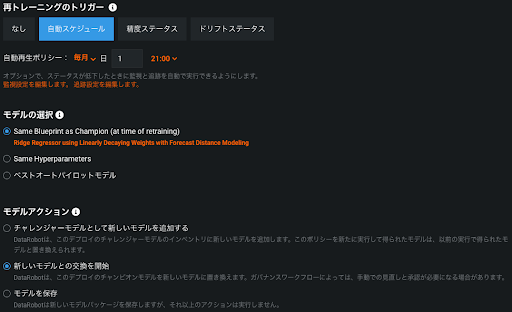
精度の劣化やデータドリフトが検知された場合、あるいはそういったシグナルが検知されなくても定期的に直近のデータでモデルを作り直すことは精度の維持に置いて有効な手段です。DataRobot では図11のように定期的スケジュールや精度・データドリフトのステータスの変化をトリガーとしてモデルの再モデリングと置換を自動化（英語ブログ）することができます。

実運用モデルの置換の必要が生じた場合でも過去の精度や運用記録は引き継いだまま、モデルの置換を行うことができ、DataRobot の内部でデプロイと紐づくモデルが変更されるだけなので、外部システム連携するために記述されたプログラムに修正を加える必要はありません。

おわりに

本稿では需要予測を最適な発注量に繋げる方法を説明しました。変化が激しくデータや取り巻く状況が複雑な実際の現場で需要予測をスケールさせ、在庫最適化につなげていくためのベストプラクティスのひとつとして、人間が工数をかけるべき箇所と自動化できる箇所の棲み分けの明確化があります。そして、DataRobot はその自動化を多くの部分で実現可能にします。需要予測とそれを活用した在庫最適化は一朝一夕には達成できない根気のいるプロジェクトですが、人と AI の担当を明確にし協力すれば着実に効果に結び付けられるユースケースでもあります。DataRobot は進化し続けるプロダクトと共に、需要予測に取り組まれるお客様を引き続きサポートしていきます。

メンバー募集

DataRobot では AI の民主化をさらに加速させ、金融、ヘルスケア、流通、製造業など様々な分野のお客様の課題解決貢献を志すメンバーを募集しています。AI サクセスマネージャ、データサイエンティスト、AI エンジニアからマーケティング、営業まで多くのポジションを募集していますので、興味を持たれた方はご連絡ください。

参考文献

1. 山口雄大（2018）『この1冊ですべてわかる 需要予測の基本』日本実業出版社
2. 淺田克暢、岩崎哲也、青山行宏（2005）『在庫管理のための需要予測入門』東洋経済新報社
3. 大野勝久（2011）『Excelによる生産管理―需要予測、在庫管理からJITまで』朝倉書店
4. 勝呂隆男（2003）『適正在庫の考え方・求め方』日刊工業新聞社
5. 勝呂隆男（2006）『適正在庫のテクニック』日刊工業新聞社
6. 勝呂隆男（2014）『売上を伸ばす 適正在庫の定め方・活かし方』日刊工業新聞社