オフセット項を利用して機械学習モデルにビジネスロジックを組み込む

DataRobot で金融業界のお客様を担当しているデータサイエンティストの小川幹雄です。

機械学習が世の中で広まる中で、様々なバックグラウンドの方がデータサイエンティストとしてモデルを作成しています。昔は計量経済学などの統計バックグラウンドを持った方が多かったですが、ライブラリの充実や AutoML の登場によって統計バックグラウンドを持たない方も増えてきています。

今回紹介するオフセット項は、統計バックグラウンドの方ならばご存知の方も多いかと思いますが、モデルにおいてパラメータを学習させない特徴量を利用するテクニックです。一見、自動でパラメータを学習してくれる機械学習の良さを消しているオフセット項ですが、このテクニックを利用すると、より幅広く機械学習を利用できるようになりますので、本稿ではその使い所を解説したいと思います。

なぜ今オフセット項について学ぶのか

オフセット項に関して取り上げている最近の書籍は正直多くはありません。実は入門書的な本でも取り上げられるテクニックであるにもかかわらず、機械学習が広まる中で知名度を獲得できなかった理由はなんでしょうか。筆者の個人的な推察としては、機械学習アルゴリズムを主軸としたモデリングがマジョリティを占める中、GLM（Generalized Linear Model、 一般化線形モデル）を一度も使ったことがない人が増えていることが原因だと考えています。実際、多くの場面で機械学習アルゴリズムは大幅に GLM の精度を超えてきました。それに伴い、GLM は廃れ、オフセット項も目にする機会が減ってきたと考えています。

ただ最近この流れが少し変わってきたと思っています。COVID-19 の影響で、単純に「精度がいいモデルを使えば大丈夫」が成り立たないケースが増えてきました。このようなケースでは過去データをシンプルに学習させるだけでなく、この先の未知の状況を加味した補正や物事の構造をモデルに反映させていくこと、すなわち「GLM が得意だったこと」が求められています。今のような時代だからこそ、機械学習アルゴリズムを主軸として利用していたデータサイエンティストにも古典的なオフセット項のような技術も身につけていただくのが良いのではないかと感じて今回のテーマとさせていただきました。

オフセット項での予測値の振る舞い

ここからオフセット項の振る舞いについて簡単な数式を利用して紹介していきます。数式が苦手という方でも、オフセット項にどのような値を入れるとどのように予測値が変化するかも合わせて解説していくので、実際にどのように予測値が変化するのかというポイントを手元でも試していただけるとわかりやすいかと思います。

オフセット項 Offsets の振る舞いはリンク関数 linkfunction、ターゲットのベクトルY、特徴量のベクトルX、パラメータβに対して以下のような数式で表されます。

linkfunction(Y) = Offsets + Xβ

オフセット項にはパラメータがついていないので、モデルの学習時にターゲットに対しての関係性が更新されることはありません。もう一つ大事な特徴としては、オフセット項はリンク関数の影響は受けるので、リンク関数の種類によってターゲットに対しての振る舞いが変わってきます。今回は連続値問題と二値分類問題において予測値がどう振る舞うかについて説明していきます。

連続値問題

連続値問題では、リンク関数に log 関数が使われているかいないかがポイントになります。DataRobot ではターゲットの分布に対して自動的に最適化指標が決められますが、最適化指標が RMSE の場合には、リンク関数は identity（そのまま）となるので、以下の数式のようにオフセット項の値はそのまま予測値に足し合わされるだけのものとなります。あまりこのパターンでオフセット項を使うメリットはありません。

Y = Offsets + Xβ

次に、Poisson Deviance、Gamma Deviance、Tweedie Deviance が選ばれている場合には、リンク関数は log 関数が使われます。この場合には、以下の数式のように exp^Offsets は掛け算した関係になります。

log(Y) = Offsets + Xβ

Y = exp^{Offsets + Xβ} = exp^Offsets x exp^Xβ

よって、オフセット項の値を自然対数表に合わせて設定することによって予測値をコントロールすることができます。オフセット項を0.40547にするとexp^0.40547=1.5より予測値が1.5倍、0.69315にするとexp^0.69315=2より予測値が2倍になります。人口と面積から人口密度が出る関係のように、予測値との関係が割り算で表せられるケースにおいては、リンク関数に log 関数を使った上でオフセット項を利用することによって、割り算の関係性をそのままモデルに組み込むことができます。

二値分類問題

次に二値分類問題のときについて解説していきます。二値分類ではリンク関数はlogit 関数となり、オフセット項は以下の数式のような関係性になり、exp^Offsets がオッズ（確率pにおけるオッズ=p/(1-p)）に対してかかる関係性になります。

logit(Y) = Offsets + Xβ

log(Y/1-Y) = Offsets + Xβ

Y/1-Y = exp^{Offsets + Xβ} = exp^Offsets x exp^Xβ

例えば、オフセット項を0.40547にするとexp^0.40547 = 1.5より、オッズが1.5倍になります。これは予測値が0.5の場合、オッズは0.5/(1 – 0.5) = 1となります。オッズが1.5倍なので1.5 = y/(1 – y),0 ≤ y ≤ 1となり、予測値は0.6となります。

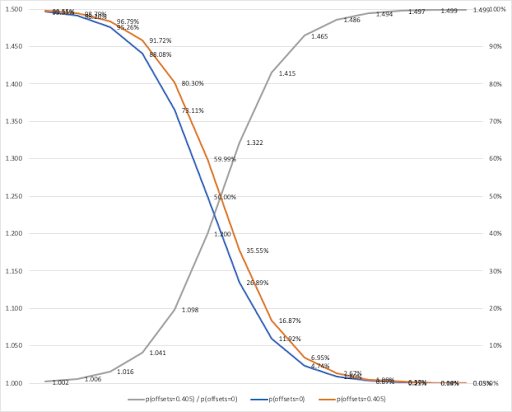
参考までに以下にオフセット項が0(exp⁰ = 1)でベースとなる予測値を青い線、オフセット項を0.40547(exp^0.40547 = 1.5)としたときにベースとなる予測値から変化した予測値をオレンジの線、ベースとなる予測値とオフセット項によって変化させた予測値の比をグレーの線で表したチャートを記載します。二値分類ではオフセットはオッズにかかることから、予測値が小さいときほど比率としては予測値に与える影響は大きく、予測値が大きいほど比率としては予測値に与える影響が小さくなることがわかります。

オフセット項の活用例

以下、オフセット項を活用するケースを3つ紹介します。一つ目は(1)特定の関係性をもつことが自明でそれをモデルに組み込んだ上でモデリングを行いたいときです。二つ目は、(2)学習データには存在しない入力においても予測値をコントロールしたいときです。この二つにおいては設定するロジックがしっかりと自明のものである必要があります。最後の一つは、(3) 一定レベルの構造知識がある場合に、その構造をモデルに残したいときです。完全に関係性を把握していなくとも、一定レベルの構造知識がある場合に、その構造を残したままモデリングできるテクニックです。

(1)自明の関係性をモデルに組み込む：

「データ解析のための統計モデリング入門」のオフセット項の説明でも出てくる、予測ターゲットが密度やコンバージョン率など、それぞれが面積や回数などと割り算の関係性を持っている割算値のケースです。本稿では Web 広告などでよく使われるコンバージョン率の分析を行いたいときの例で考えていきます。CV rate がコンバージョン比率、Con がコンバージョン数、Click が合計クリック数とすると、

CV rate = Con/Click

CV rate に対するモデルを作ることを考えると以下のような数式になります。

CV rate = exp^Xβ

Con = Click x exp^Xβ = exp^log(Click) x exp^Xβ = exp^{log(Click)+Xβ}

log(Con) = log(Click) + Xβ

数式からも log(Click) がコンバージョン数をターゲットにリンク関数に log 関数を利用した時のオフセット項と一致することがわかります。

具体的な例として、金融業界でよく行われているデフォルト予測や保険金請求額予測などの例について考えていきます。これらは同じ状態であれば観測期間が長いほど発生確率が高いと考えられます。この際に、学習データで観測期間を揃えたり、ターゲットを期間で割ってあげるなどのアプローチも考えられますが、それでは、トータルとしての金額などのスケール情報を失ったり、元の分布を歪めてしまうことに繋がります。

以下の図で表しているように、各契約期間における単位金額に変換する場合に、契約期間1年を1として、契約期間ごとにオフセット項をセットしていきます。1年を1としたときのそれぞれの契約期間は、データ抽出のタイミングにおいて契約 A では1年間の契約が終わっているので1(オフセット項 = log(1) = 0)、契約 B はまだ契約が始まったばかりで1ヶ月しか経ってないので、1/12 = 0.083(オフセット項 = log(0.083) = -2.4889)、契約 C は18ヶ月なので18/12 = 1.5(オフセット項 = log(1.5) = 0.4054)、契約 D は途中で解約があったため6ヶ月で6/12 = 0.5(オフセット項 = log(0.083) = -0.6931)となります。

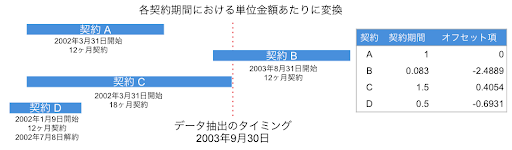
オフセット項を利用することによって、自明のロジックをモデルに組み込み、契約期間以外の要素がどれくらいしっかりと効いていたのかを正しく分析する事ができます。（本稿の後半では実際に DataRobot を利用した分析手順を紹介します）

ただし作成されたモデルの精度だけを比較した場合には、オフセット項を利用せずに学習したモデルのほうが検定データにおける精度では高い傾向にありますので、オフセット項が手元のデータにおける精度を必然的に上げるテクニックではないということは覚えておいていただくと良いと思います。

(2)学習データに存在しない特定の入力に対しての予測値を制御する：

予測値を特定の入力に対してコントロールしたいケースは、学習データに存在しないまたはあまり出てこない値に対応させたい場合に有効です。コロナ禍によって戦後GDPが過去最悪となりましたが、GDP を特徴量として倒産予測などを行っている場合では、GDP が学習データにないレベルまで悪化した場合に、他が同じ状況であれば GDP がよい状況よりも倒産確率が高く出ることが望ましいでしょう。ほかにも融資範囲の拡大などによって、これまでの機械学習用の学習データには存在しないが、ビジネルロジックとして補正するルールを持っている場合に、そのルールをモデルに反映させたいときがあります。

モデリングのフェーズでは(1)と同じ様にオフセット項を設定して学習させます。オフセット項はパラメータを学習させない特徴量であるがゆえに、予測時において、学習データに含まれていない入力があったとしても、予測値を想定の動きにコントロールすることができます。

特に、カテゴリデータにおける未知のクラスへの対応においてオフセット項は効果的です。オフセット項を利用しない場合には、カテゴリデータの未知なクラスへの対応としては、学習時に「その他」などのクラスを作っておき、未知のクラスをすべて「その他」クラスと扱うのが一般的です。ただ、この手法では未知のクラスが良くも悪くも「その他」と同じ扱いにしかならないので、重要なクラスが将来に登場する場合には微妙なモデルとなります。オフセット項をカテゴリに利用することによって、未知のクラスであってもモデルをドメイン知識に従い、思った方向にコントロールすることができるようになります。

(3)2段階モデリング+オフセット項でモデルに構造性をもたせる：

ある特定の特徴量セットが構造的に必ず影響することは知っているが、他に影響する特徴量はわからないケースにおける分析では、2段階モデリングにオフセット項を利用するテクニックを適用できる場合があります。特にデータ量が多くないにもかかわらず多くの特徴量が利用できる場合、すべての特徴量を学習に利用すると、重要視してほしくない特徴量を重要視して、重要視してほしい特徴量は重要視しないというモデルができる可能性があります。このような場合に、特定の特徴量は半強制的にモデルに組み込む必要がある(重要視したい)というドメイン知識があるならば、下図のような「2段階モデリング＋オフセット」という技が有効です。

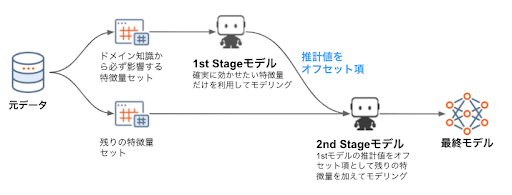
• 1段階目(1st Stage)：ドメイン知識から有効と理解している特徴量のみを選択してモデルを作成
• 2段階目(2nd Stage)：1段階目のモデルの予測値をオフセットとして、残りの特徴量＋オフセットで学習

このステップを踏むことによって、ドメイン知識から優先的に効かせたい特徴量をモデルに効かせやすくする事ができます。

上記は DataRobot 立ち上げメンバーでアクチュアリー出身の Xavier Conort が Kaggle で実際に利用したテクニックでもありまして、日本アクチュアリー協会の例会で彼がプレゼンした資料でも紹介されています。

DataRobot におけるオフセットの設定

それでは、DataRobot を利用してオフセット項を含むモデルを作成する手順を以下解説します。

データ準備

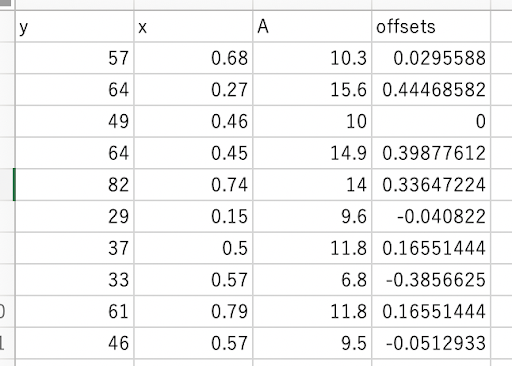
学習データでは、どの特徴量(列)をオフセット項とするかを決めます。その後は、特徴量の各値に対してのターゲットの関係性を数値で入れていきます。オフセット項は以下の性質を満たす必要があります。

• すべて数値
• 十分なカーディナリティを持った値(すべて同じ値は NG)
• 欠損値を含んでいないこと

注意点として、オフセット項のターゲットとの関係性は先の章で解説したようにリンク関数によって変わってくるので、どのリンク関数が使われるのか意識する必要があります。また、もしオフセット項扱いとする特徴量がデータセットに含まれている場合には、そちらは除いておきます。

DataRobot でのモデリング設定と対応ブループリント

DataRobotにデータをアップロードしたら、ターゲットを選択し、「高度なオプション」からオフセット項を設定します。設定は「高度なオプション」->「その他」の一番下にあります。

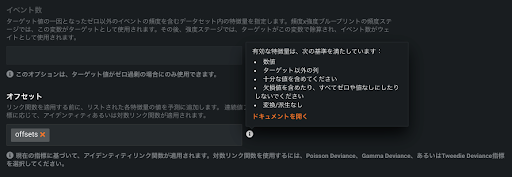
設定箇所にはオフセット項として作った特徴量名を入力します。上記画像の例だと offsets としていますが、特に名前に縛りはありません。またオフセット項は複数選択することができるので、複数の自明のロジックをモデルに組み込むことも可能です。インフォメーションボタンを押すとオフセット項として対応している形式についての説明を改めて見ることができます。

また DataRobot では、最適化指標に合わせたリンク関数が自動で選択されます。オフセット項をセットすると、現在の最適化指標でどのリンク関数が使用されるのか表示され、別のリンク関数を利用するために選ぶべき最適化指標が表示されます。オフセット項と想定したリンク関数が使用される最適化指標がセットできたことが確認できれば、今まで通りオートパイロットを開始します。

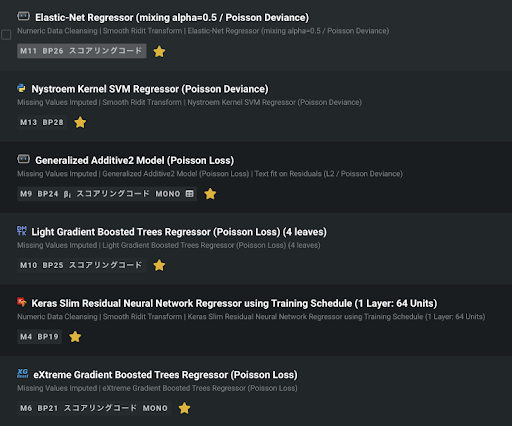
オフセット項はもともとGLMでよく使われるテクニックですが、DataRobot では GLM だけでなく、SVM や LGBM、xGBoost、Neural Net などにも対応していますので、最新のアルゴリズムに古典的なオフセット項の手法を合わせて使うということも簡単にできるようになっています。

モデル解釈

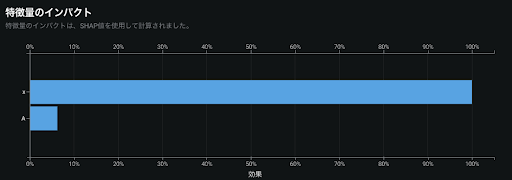
モデル解釈の部分では、オフセット項に設定した特徴量は、ターゲットに対しての関係性が自明のため、特徴量のインパクトや特徴量の作用は表示されません。オフセット項以外の特徴量に関しては、オフセット項における予測値への補正をなくした状態で通常と同じ様に計算されます。要するに純粋にオフセット項以外の特徴量の影響を見ることができるようになっています。

SHAP 値の加法性を確認したいときは、オフセット項の影響を予測値から取り除いた状態で成り立ちます。例えば、リンク関数が log 関数の場合において、オフセット項に0.33647という値を使用している場合、exp^0.33647＝1.4となるので、予測値を1.4で割った上で、SHAP 値の加法性が満たされます。

Prediction = exp^Offsets x exp^{(SHAPvalue₁ + SHAPvalue₂ + … + SHAPbasevalue)}

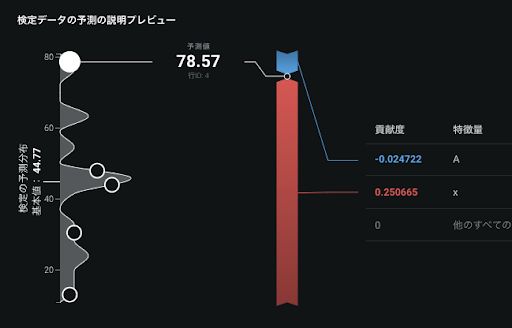
予測時の動作

作成したモデルで予測を実施する場合には、通常の DataRobot の予測のフローと全く同じで、ターゲット以外の全ての特徴量を含んだデータ（オフセット項で利用した列も含む）を利用します。

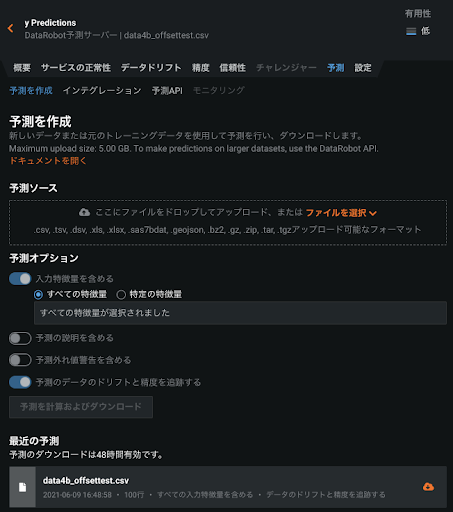
オフセット項以外の残りの特徴量の値が同じ場合に、オフセットの値を変化させることによって元々想定していた関係性通りに予測値を補正できることを試していただければと思います。

DataRobot におけるエクスポージャー

連続値問題においてオフセット項をターゲットに対して比例関係で利用したい場合、先にも紹介したように、以下のような数式となります。

log(Y ) = Offsets + Xβ

Y = exp^Offsets + ^Xβ = exp^Offsets x exp^Xβ

数式からもオフセット項を比例関係で利用するには exp^Offsets と自然対数表を見ながら設定する必要がありますが、入力データの直感性がないので、後でデータを見返すとややこしい場合もあるかと思います。

このような場合には DataRobot では「エクスポージャー」を使うとより直感的操作をすることができます。エクスポージャーは連続値問題かつリンク関数が log 関数となる最適化指標でしか利用できないという制約はありますが、エクスポージャーに0.25と入れると予測値が0.25倍、2.0と入れると2倍と直感的に利用することができます。

内部動作的にはオフセット項で行うべき変換を DataRobot 内で自動的に行なっているだけなので、用途限定の便利なオフセット項機能と思って使っていただければと思います。

exposure = exp^Offsets

注意点としては上記の式からもわかるように、エクスポージャーの値はすべて0より大きい数値である必要があります。

最後に

オフセット項を実際の機械学習プロジェクトでどれくらいの確率で採用するかと問われれば、これまでの筆者の金融業界での経験では40〜50回に1回という感覚です。しかしながらオフセット項を理解することによって、機械学習モデルをコントロールするという感覚を身につける手助けになると思います。そして、ただ手元のデータを DataRobot に学習させて検定データでのスコアを見るだけでなく、そもそも手元のデータをどのように学習させたいかという機械学習モデルをコントロールする力を身につけることによって、スモールデータでの分析であったり、正しい汎化性能をもたせたモデルの構築がよりうまくなると思います。

本稿には数式がいくつか出てきましたが、数学が苦手な方もお手元のデータセットでオフセット項の動きを試していただくと感覚がつかみやすいと思います。AutoML が盛り上がってきた今こそ、先が見通せない不透明さをカバーするのに役立つ古典的手法も引き出しとして持っておき、実践されてみてはいかがでしょうか。