DataRobotで小売・流通業界のお客様を担当しているデータサイエンティストの濱上です。
本稿では、マーケティング、ヘルスケア、公共政策などの分野での活用が期待されるアップリフトモデリングをご紹介します。アップリフトモデリングのコンセプトは目新しいものではありませんが、AI・機械学習の発展により、誰でもアップリフトモデリングを実践できるようになりました。しかしながら、アップリフトモデリングに必要なデータセットや適用範囲を理解していないと、全く意味のないモデルが構築されてしまいます。そこで、本稿では、アップリフトモデリングの注意点やユースケースを説明し、 DataRobotを利用したモデリング方法をご紹介します。
1. アップリフトモデリングとは
人生は選択の連続です。皆さんも、『もし転職すれば年収はどれくらいになるだろうか』とか、『もしジムに通えばどれくらいダイエットできるだろうか』などと考えることがあるかもしれません。ビジネスにおいても、「このユーザーにダイレクトメール(DM)を送れば購入してもらえるだろうか」とか、「値引きしなくても購入してもらえるだろうか」などと営業・マーケティング担当は日々、頭を悩ませているかもしれません。そもそも人間は2人分の人生を送れないので、「仮定のアクション」をとればどのような結果になるのかを想像するのです。
少し哲学的な話になりましたが、因果推論[1]の文脈では、現実とは反対の状況をシミュレーションすることを反実仮想といいます。本稿で紹介するアップリフトモデリングとは、まさに反実仮想の考えを用いて介入効果を予測する方法であり、マーケティング、ヘルスケア、公共政策などさまざまなフィールドで応用できます。
1−1.アップリフトモデリングの定義とメリット
一般的に、アップリフトモデルは以下のように定義されます。[2]
- アップリフトモデルとは、個別ないしサブグループごとに介入効果を予測・推論するモデルのこと。
介入効果とは、ある対象に介入したときに観察される結果Aと、同じ対象に介入しなかったときに観察される結果Bとの差のことです(図1)。例えば、あるユーザーにクーポンを送付したときの購入確率が50%、同じユーザーにクーポンを送付しなかったときの購入確率が20%のとき、介入効果は 50% – 20% = 30% と計算されます。
このように、ユーザーごとに介入効果を計算できれば、介入効果が高いユーザーに絞ってクーポンを送付することで費用対効果を改善できます。しかし、実際には、ある1人のユーザーに「介入したとき」と「介入しなかったとき」を両方とも体験してもらうことはできません。つまり、そのユーザーにクーポンを送ってしまえば、クーポンを送らなかったとしても購入したのかどうかは分かりません。
そこで、アップリフトモデルの出番です。アップリフトモデルを使って、我々がそのユーザーに「介入したとき」と「介入しなかったとき」の結果をシミュレーションし、介入効果を算出します。魔法のようなモデルと感じるかもしれませんが、モデリングに使用するデータセットを工夫すればそのようなモデルを構築することが可能です。データセットの工夫については後ほど詳しくご紹介します。

1−2.アップリフトモデリングを使うべきときとは
アップリフトモデリングは、効果検証のいかなるケースでも使えるわけではありません。
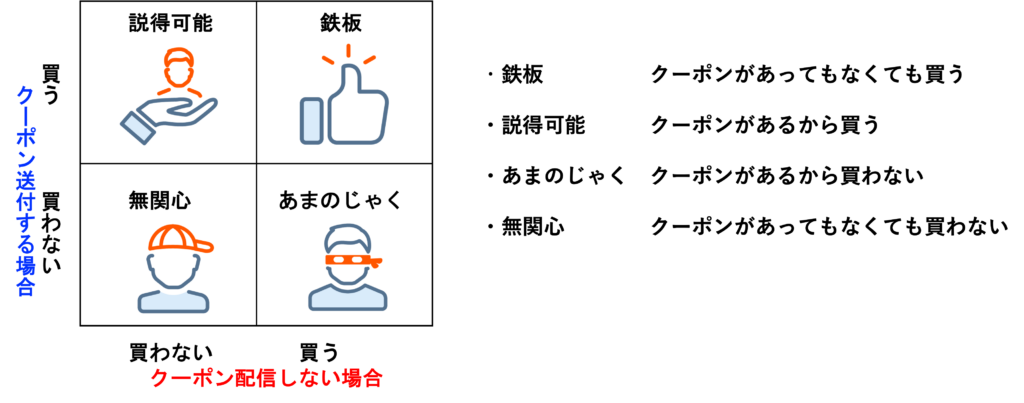
具体的に、アップリフトモデリングが適しているのは、以下のように我々が介入を検討している対象が4つのグループに分けられると想定されるときです(図2)。それぞれ見ていきましょう。
「鉄板」ユーザーとはクーポンを発行する場合も買うし、クーポンを発行しない場合も買うユーザーです。一方で、「説得可能」なユーザーは、クーポンを発行しない場合は買わないが、クーポンを発行する場合に買うユーザーです。営業・マーケティング担当者は「鉄板」ユーザーではなく「説得可能」なユーザーにこそクーポンを送付したいはずです。また、クーポンを発行しても買わない「無関心」なユーザーやクーポンの発行により逆に買わなくなる「あまのじゃく」なユーザーにはクーポンを送付すべきではありません。
介入効果の観点では、効果が大きい順に「説得可能」 >>「鉄板」,「無関心」>「あまのじゃく」という順番になります。アップリフトモデルで個々のユーザーの介入効果を推定して達成したいことは、「説得可能」なユーザーの選別です。
1−3.レスポンスモデルとの比較
アップリフトモデリングは上図のように4つのグループがあるときに適していますが、世の中には「鉄板」が存在しないケースがあります。例えば、新しいブランドで、世間にまったく認知されていない製品です。
このようなケースでは、何もせずとも買ってくれるような「鉄板」ユーザーはいないので、広告やプロモーションなどの介入を行うことが前提となります。そのため、これから介入すべきユーザーを選定するためには、これまでに介入した時の結果のデータのみを使用してモデリングします。このモデルは、介入したユーザーの中で、どのようなユーザーがレスポンス(=購入)する確率が高いのか学習し、予測するモデルなのでレスポンスモデルと呼ばれます(表1)。[3]
一方で、アップリフトモデリングでは、介入しなくても購入する「鉄板」がいるため、介入したデータ(介入群データ)に加えて、介入していないデータ(対照群データ)もモデリングに利用します。介入していないユーザーの中で、どのようなユーザーが購入する確率が高いのか学習させるためです。
モデル構築を担当する分析者は目の前の状況がどちらのユースケースに適しているのか見極めて両者を適切に使い分けることが大切です。

ここから、DataRobotを用いてアップリフトモデルを構築するための手順をご紹介します。まず、アップリフトモデリングの成功に欠かせないデータセットの工夫について話します。
2−1.データ準備
アップリフトモデリングでは、介入群データと対照群データを使用すると述べました。ここで重要なのが、介入対象となるユーザーの選択にバイアスがあってはいけないという点です。では、なぜ、このような「選択バイアス」があるといけないのでしょうか。
例として、外食デリバリーサービスの利用を促すDMを各世帯に送付するケースを考えます。このサービスの購入には、世帯人数、平均年齢、世帯収入、居住地、リモートワークの有無、夫婦共働きか、など様々な因子が関係していそうです。例えば、共働き世帯は外食デリバリーサービスを利用しやすいかもしれません。(なお、疫学分野ではこれらの因子を『曝露因子』と呼びます。)
そこで、共働き世帯に絞ってDMを送付したとします。その結果、思惑どおり、DM送付した世帯は、DM送付していない世帯よりも全体としてサービスの購入確率が大きいことが分かりました。しかし、その購入確率の差は、DM送付が功を奏したからなのか、単純に共働き世帯が購入しやすいからなのか、それとも世帯収入などその他の因子が影響したからなのか判別できません。
この状況を図で表すと次のような関係となります(図3)。原因から結果に向けて矢印が伸びています。われわれは、「DM送付」と「購入」の間の因果関係を知りたいのに、上記の仮想ケースでは「共働き世帯か」という尺度でDM送付対象を決めてしまったが故に、注目している因果関係の大きさ(=介入効果)を見積もることができなくなっています。
このように介入対象の選択にバイアスがかかってしまうと介入効果を正しく計ることができません。なお、ここで「共働き世帯か」のように、注目している要因にも結果にも影響する因子のことを交絡因子といいます。交絡因子がある状況でどのように因果推論するのかについては弊社ブログ「機械学習を用いた要因分析(理論編1、理論編2)」で詳しく解説しています。

それでは、選択バイアスのないデータを準備するにはどうすればいいでしょうか。理想はランダム化比較試験(RCT)を実施することです。[4] RCTでは、母集団を介入群と対照群にランダムに振り分けます。しかし、実世界においては選択バイアスがかかったデータしか手元になかったり、そもそも倫理的・コスト的にRCTが難しかったりするケースが見られます。そこで、観察データを用いた観察研究の文脈において選択バイアスを取り除くための方法として層別化や傾向スコアマッチングなど様々な手法が知られています。弊社ブログ「機械学習を用いた要因分析(実践編)」では、DataRobotを用いた傾向スコアマッチングのやり方をご紹介していますので、ぜひご覧ください。(なお「機械学習を用いた要因分析(理論編2)」に記載があるように、重要な交絡因子を網羅していることがこの手法を適用するための前提条件となるので、その点は十分にご留意ください。)
選択バイアスの影響が無視できると考えられるデータセットを準備できてはじめてアップリフトモデリングを構築することができます。それでは、バイアスのないデータセットが準備できたとして、DataRobotでどのようにモデリングするのかご紹介します。
2−2.モデリングと予測実行
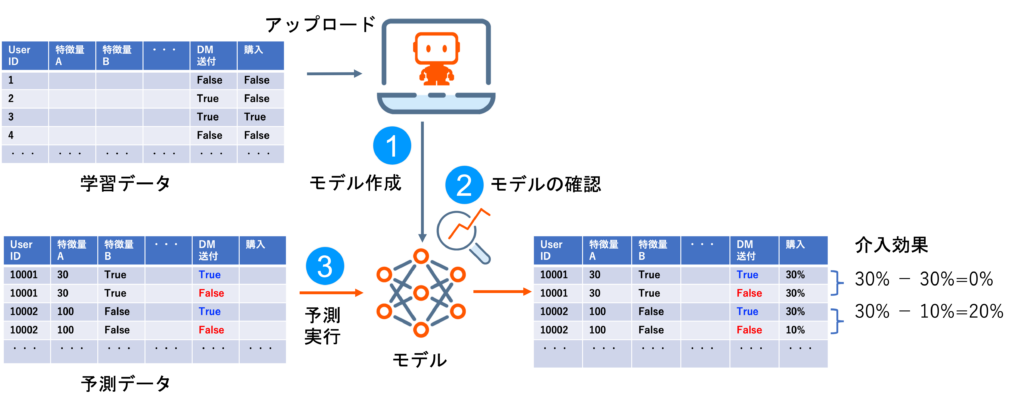
DataRobotはシンプルなユーザーインターフェースでAIモデルを作成でき、モデル評価やインサイト確認、予測実行までスムーズに行うことができます。アップリフトモデリングでも基本的なモデリング手順は変わりません(図4)。
まず、学習データをDataRobotにアップロードしモデルを作成します。なお、ここで使用する学習データは、母集団をランダムに介入群(DM送付=True)と対照群(DM送付=False)に分けてDMを送付した結果、各ユーザーが購入したかどうかTrueまたはFalseでラベル付けしたものです。[5]
次に、モデルの中身(インサイト)を確認します。
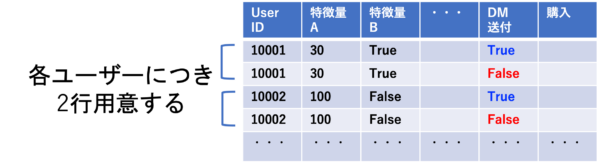
最後に、予測データをモデルに投入し、各ユーザーごとに介入効果を予測します。ここで、予測データは各ユーザーにつきDM送付=Trueの行とDM送付=Falseの行を用意します(図5)。このように2行用意することで、同一人物に「介入したとき」と「介入しなかったとき」の2パターンをシミュレーションすることができるのです。その2パターンの購入確率の差が、介入効果になります。この図では、UserID=10001の介入効果は0%に対し、UserID=10002の介入効果は20%であるため後者にDMを送付したほうがよいと判断できます。
①モデルの作成
まず、学習データをDataRobotにアップロードします。アップロードが完了すると以下のようなモデリング設定画面に移行します(図6)。何を予測しますか?に予測ターゲットを入力します。本データセットでの予測ターゲットは「購入」です。次に、開始ボタンを押してモデリングを開始します。

②モデルの確認
モデリングが終了するとモデルの順位表であるリーダーボードの画面に移行します。リーダーボードでは各モデルの予測精度やインサイトを確認できます。
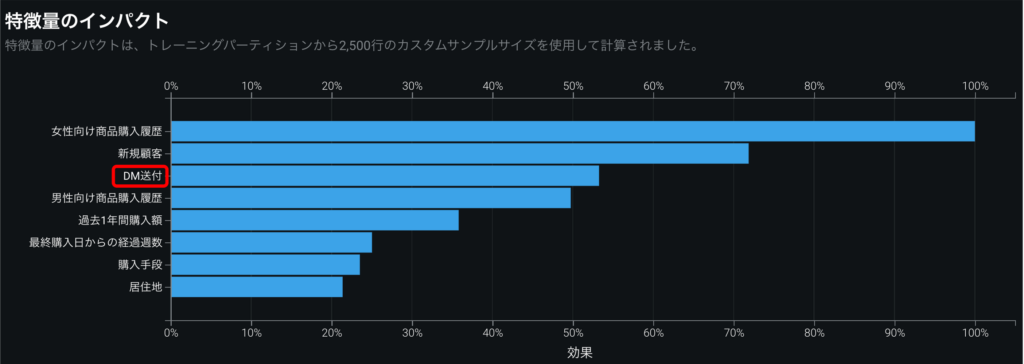
それでは、1つモデルを選択し、解釈タブを開いてインサイトを確認します。まず、知りたいのは、「DM送付」が「購入」に対してどれくらいインパクトがあるのかです。そのインパクトは特徴量のインパクトで確認できます(図7)。グラフの縦軸は特徴量の名前、横軸は相対的なインパクトの大きさを示しています。
グラフから「DM送付」は3番目にインパクトが大きい特徴量であることが分かります。仮に、「DM送付」のインパクトが非常に小さいときは、DM送付による効果が実際にはあったとしても、大きな効果として予測値に反映されないため介入効果の解釈が難しくなります。その場合は、もしインパクトの大きい交絡因子があればその特徴量で層別し、それぞれの群のデータでモデリングする(層別分析[6])などの工夫が必要です。
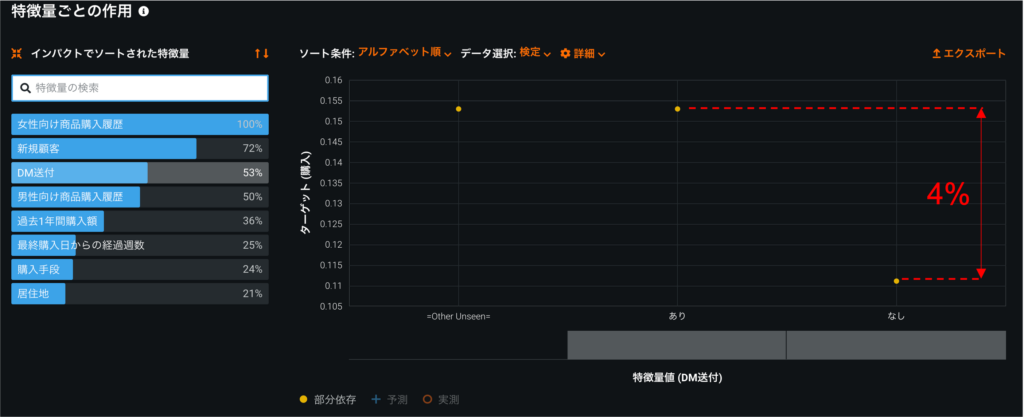
特徴量のインパクトから、「DM送付」が「購入」に対してどれくらいインパクトがあるのかを確認できます。一方、この情報からは「DM送付」と「購入」の間にどのような関係性があるのかまでは分かりません。そこで、特徴量ごとの作用を確認します(図8)。
特徴量ごとの作用では、DM送付=TrueのときとDM送付=Falseのときで、購入確率にどれくらい差があるのか分かります。DM送付=Trueのときのほうが約4%購入確率が高いことが分かりますね。しかし、これは、あくまでデータ全体の平均的な傾向です。ユーザーの中には、DM送付が購入意思に影響しない「鉄板」や「無関心」のユーザーもいるかもしれませんが、特徴量ごとの作用ではユーザーごとの介入効果は分かりません。そこで、次に、ユーザーごとの介入効果を予測してみましょう。
③予測実行
それでは、実際にDataRobotを使って介入効果を予測します。今回は最初にアップロードしたデータの20%に相当するホールドアウトをダウンロードし、介入効果を予測するための予測データを作成しました。
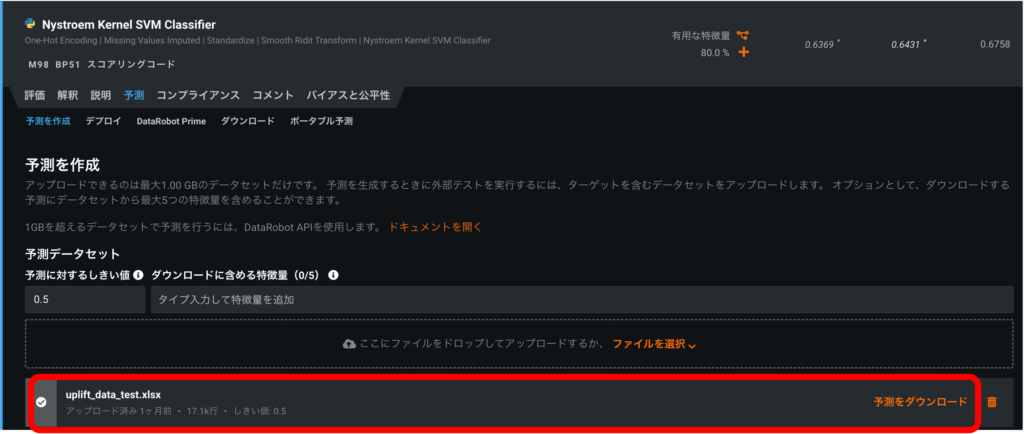
予測データを予測を作成にアップロードし、予測を実行→予測をダウンロードの順にクリックし(図9)、CSV形式で予測値を確認できます。最後に、DM送付=Trueのときの予測値とDM送付=Falseのときの予測値の差をとって、各ユーザにおける介入効果を算出します。
2−3.モデル評価
各ユーザーの介入効果の予測値を表に示します(図10)。この表では予測された介入効果が大きいユーザーから順にソートしてあります。したがって、上から順にDM送付していくことで高い費用対効果が得られると期待できます。
一方で、果たして本当に、表の上に並ぶユーザーほど介入効果が大きいのか疑問に思いませんか?そこで、介入効果の実測値を算出してみましょう。この予測データには、各ユーザーが購入した(購入=True)か購入していない(購入=False)かの実測値があるので、介入効果の実測値を算出できます。なお、予測データも介入群と対照群の分け方にバイアスがない、もしくは補正されたものを使用する必要があります。(さらに、予測データに属する群と学習データに属する群の間にバイアスがないことも前提となります。)
それでは、介入効果の実測値を算出します。まず、この表を使って、上から順にグループ0、グループ1‥‥グループ9というように10個のグループに分けます。グループの数は任意です。次に、各グループの中で、DM送付=Trueのユーザーの購入確率の平均とDM送付=Falseのユーザーの購入確率の平均を計算します。グループ0ではそれぞれ25%、16.6%と算出されます。次に、その差をとることで介入効果の実績値を算出します。25%-16.6%=8.4%が介入効果の実績値です。一方で、各グループで介入効果の予測値の平均を算出します。グループ0では予測値の平均は8.0%になります。

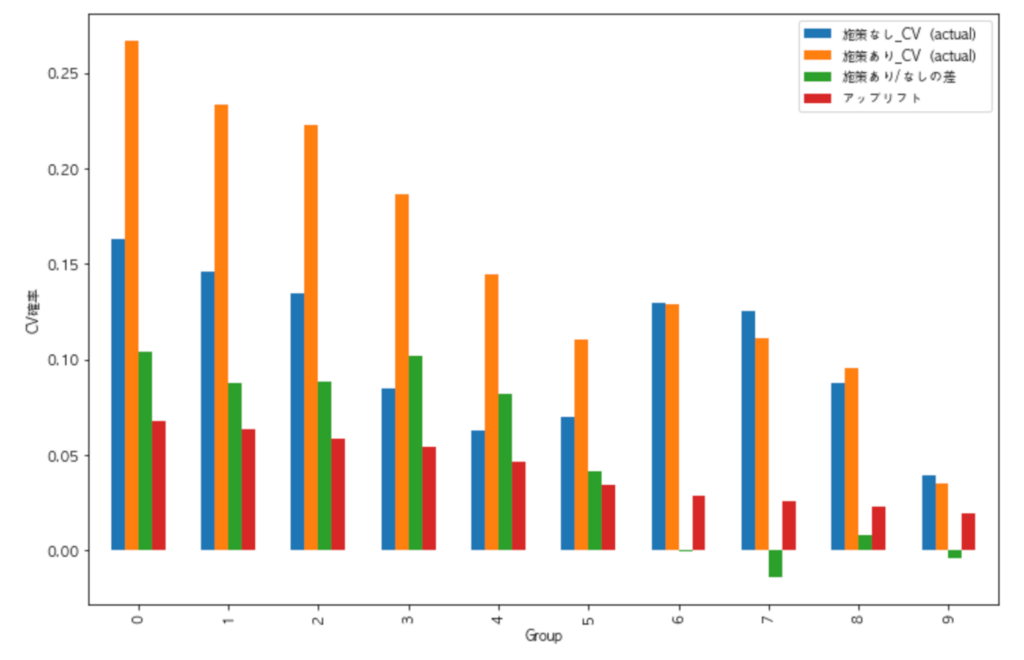
その他のグループ1~9でも同様に介入効果を計算します。その結果が以下のグラフです(図11)。横軸がグループで、縦軸が購入確率です。青とオレンジのバーが、DM送付=TrueないしDM送付=Falseのときの平均購入確率(実測値)で、緑のバーがその差の介入効果の実測値です。そして、赤のバーが介入効果の予測値の平均となっています。緑と赤のバーを比較すると、赤の予測値が小さくなるにつれて、緑の実績値も小さくなっていることが分かります。予測が当たっている証拠です。
さらに、グラフをよく見るとグループ5までは介入効果の実測値はプラスですが、グループ6以降はゼロまたはマイナスになっています。したがって、グループ6以降のユーザーにDMを送付しても、それによる効果は見込めないことが分かります。言い換えると、アップリフトモデルにより、DMを送付すべきユーザーを全体の60%に絞り込むことができたのです。
DM送付には、作成、印刷、郵送費などのコストがかかりますので、ユーザー全員に送付するのに比較して40%もコストを削減することができ、且つ同じだけの効果が得られることになります。このように、グラフを描くことで、介入効果が高いグループを絞りこめているか判断できます。なお、複数のアップリフトモデルの精度を比較したいときは、The Area Under the Uplift Curve(AUUC)[7]やQini係数[2]などの評価指標で比べるほうがより細かな差を判定できます。
3. まとめ
以上、アップリフトモデリングのコンセプトからDataRobotを用いたモデリングおよび予測実行までご紹介してきました。本稿で述べたことをまとめると以下になります。
- アップリフトモデリングの成功のためには、ユースケースを把握し、データ準備においては選択バイアスのないもしくは取り除いたデータを用意することが必要不可欠である。
- DataRobotを用いれば、シンプルな操作でアップリフトモデルを構築でき、予測実行まで簡単に行える。
皆様の業務においてアップリフトモデリングの活用イメージが膨らんでおりましたら幸いです。
参考文献
- 因果推論の入門書として以下の書籍をお薦めいたします。
- データ分析の力 因果関係に迫る思考法 (光文社新書), 伊藤 公一朗 (著)
- 岩波データサイエンス Vol.3, 岩波データサイエンス刊行委員会 (編集)
- Gutierrez, P., Gérardy, J. Y. (2017) Causal Inference and Uplift Modelling: A Review of the Literature. Proceedings of The 3rd International Conference on Predictive Applications and APIs, 1-13.
- Radcliff, N. (2007) Using control groups to target on predicted lift: Building and assessing uplift model. Direct Market J Direct Market Assoc Anal Council, 1:14–21.
- RCT大全 ランダム化比較試験は世界をどう変えたのか(みすず書房),アンドリュー・リー(著),上原裕美子(訳)
- Kevin Hillstrom’s dataset from E-Mail Analytics And Data Mining Challenge(2008)で公開されているデータセットを一部加工
- 岩波データサイエンス Vol.3, 岩波データサイエンス刊行委員会 (編集) p.17-20
- Jaskowski, M., Jaroszewicz, S. (2012) Uplift modeling for clinical trial data. In ICML Workshop on Clinical Data Analysis
Related posts
See other posts in データサイエンスRelated posts
See other posts in データサイエンスGet Started Today.